OptiStruct随机振动分析 原理 PSD应力 RMS应力 1σ应力 概念解释

随机振动分析结果的解释 文|澳汰尔 王维金

写在前面：

随机振动分析和频响分析

随机振动与频响分析相比：

随机振动的输入为功率谱密度（无明确相位）；频响分析输入为频谱（幅值+相位），即可以理解为相位的随机性

随机振动的输出也为功率谱密度（无明确相位）；频响分析的输出也为频谱（幅值+相位）

鉴于随机振动的相位随机性，随机振动分析得到的频域结果，可以回归等效（逆变换）为一系列的时间历程曲线，其集合可以得到一个完整的随机过程。而频响分析的结果可以回归等效（逆变换或者傅里叶级数叠加）至唯一的时间历程曲线，也就是我们常说的确定性过程。

鉴于上述的原因，对于随机振动分析，我们只能用统计学的角度去得到一些有意义的结果，而不是能像频响分析一般，可以直接得到应力幅值、最大值等明确性指标。

随机振动分析关心的结果

对于要得到统计学上的指标，首先我们得知道激励或者响应是服从什么分布的，否则也无从谈起统计学指标，然而对于我们的现实生活，大部分的自然/物理现象都服从正态分布（高斯分布），因此对于随机性研究我们也假设我们的输入是服从高斯分布的（当然大多数情况也是自然满足的）。因此随机振动分析准确的说我们研究的是高斯随机过程。

高斯分布及随机振动分析的假设

对于高斯分布，有两个基本参数：均值和标准差，知道了这两个参数就可以得到高斯分布的概率密度曲线，进而基于概率密度曲线可以得到该曲线对应的一系列事件（这里可以认为是我们的时域曲线）他的均值、分布概率、每个值所发生的概率等等。

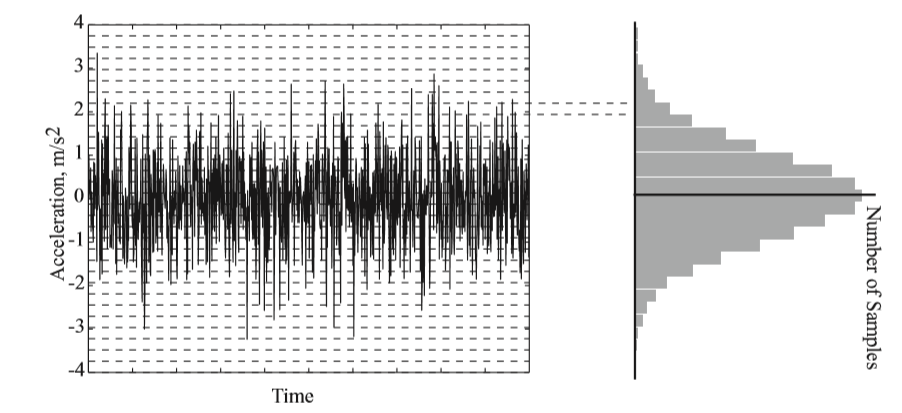
如上图，知道了高斯分布参数，我们就可以知道某一个时间发生的概率，比如图上当响应为2m/s^2时，其发生的概率是多少。

对于高斯分布，如果均值为零，那么就只有一个标准差参数了，我们仿真中也有这样的假设，而且他从软件计算层面也是先天满足的。首先一般我们给定的功率谱密度，往往在0Hz处是0；0Hz的值代表的就是均值；即便我们给的载荷在0Hz处不为零，OS也是无法计算和输出0Hz处的结果的，也认为他是零。所以他在os里是先天满足的。

因此，我们经常讲在随机振动分析中有两个基本假设就是：

-载荷和响应都服从高斯分布（正态分布）

-零均值假设

可见，鉴于这个合理假设。对于我们的随机振动分析，我们可以理解为我们就是想得到标准差！知道了标准差就知道了具体的高斯分布过程，那么就可以知道其概率分布。

标准差和RMS

标准差的公式见下，由于零均值，所以他就等于均方根值，或者叫做有效值RMS，所以一般情况下我们都不加区分的说rms应力，其实他指的就是1σ应力。

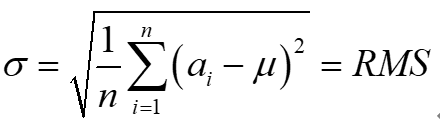
为什么要用随机振动分析

上述阐述了随机振动分析和频响分析的差异，以及对于随机振动分析我们只能得到统计意义上的结论，那么为什么我们会要用随机振动分析代替频响分析呢？原因可以归结为以下几类：

1. 频谱载荷是通过包络得到的，通过包络产品在整个服役期间各类载荷，得到一个包络谱，也就是说该包络谱涵盖了所有的载荷可能性，这样得到的载荷谱往往是在相位上无表征的，也就是随机的，通常是功率谱密度，因此自然也就是用随机振动分析，如一些标准提供的载荷谱曲线

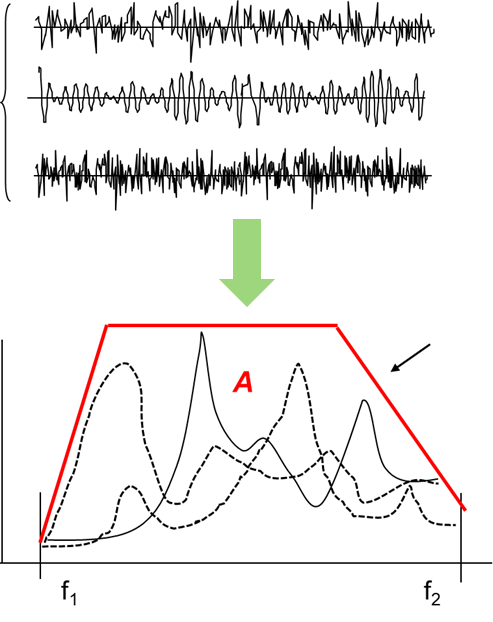
1. 激励本身具有随机性，我们往往测的是其中的一段而已，如果我们想得到完整的激励的响应，那么就用随机振动分析，当然有个前提假设就是各态历经；也就是这一段激励在时间上的特性可以模拟空间上的特性。
2. 考虑激励之间的相干

如何求RMS

前面提到了我们想要通过随机振动分析得到标准差σ或RMS值（后续将不再刻意区分），进而得到确定的高斯过程，得到一些统计学结论。

然而对于随机振动分析，我们是在频域进行分析的，激励是功率谱密度，响应也是功率谱密度，那么如果通过功率谱密度曲线得到RMS值呢？

这里就用到信号处理中一个重要的定理：帕塞瓦尔定理

帕塞瓦尔定理描述的是能量的守恒，即信号的总能量等于各个分量的能量之和，或者说能量是守恒的，不在乎是在时域表达或者频谱表达。

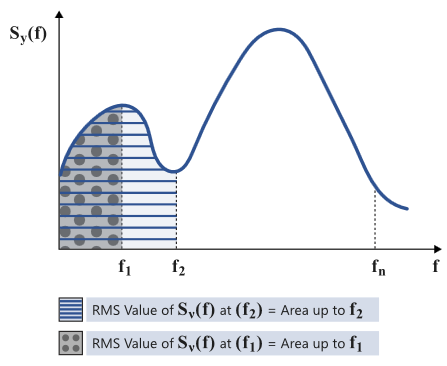
能量在时域中往往通过均方值来表达，下图左式/T就是均方值，右侧/T之后积分内就是功率谱密度的定义，RMS值均方根值即均方开根号，也就是说功率谱密度积分（也就是PSD谱下的面积）开根号就是我们想要得到的RMS值。

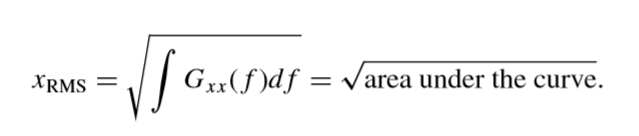
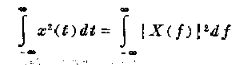
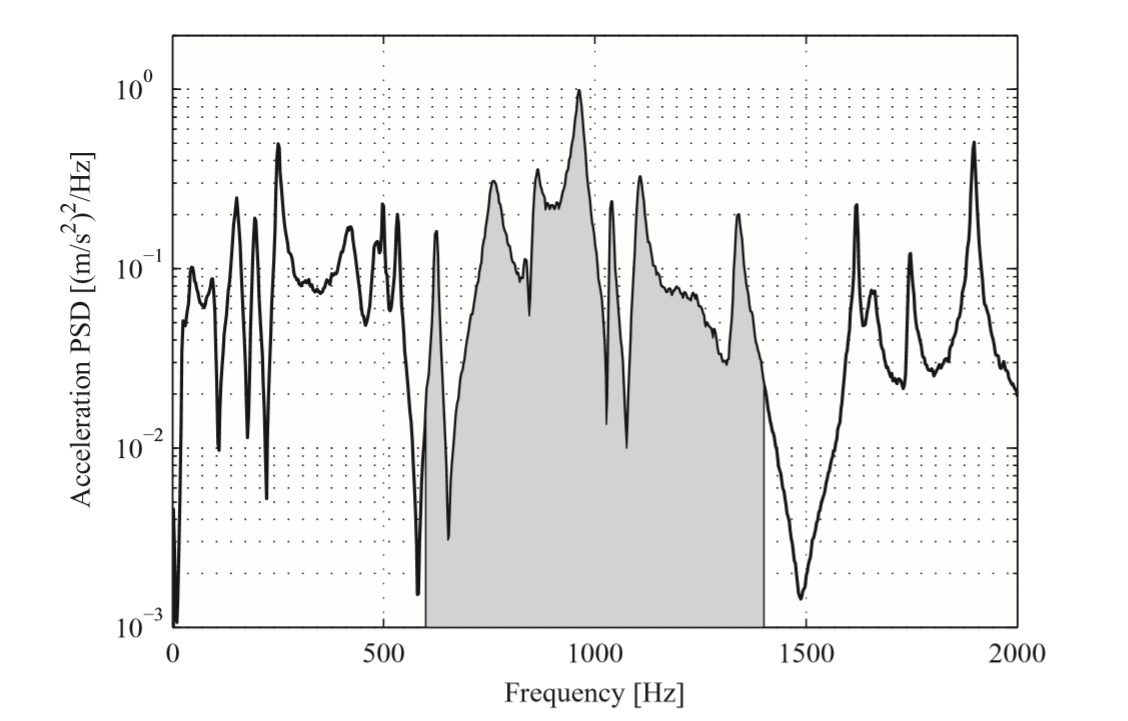
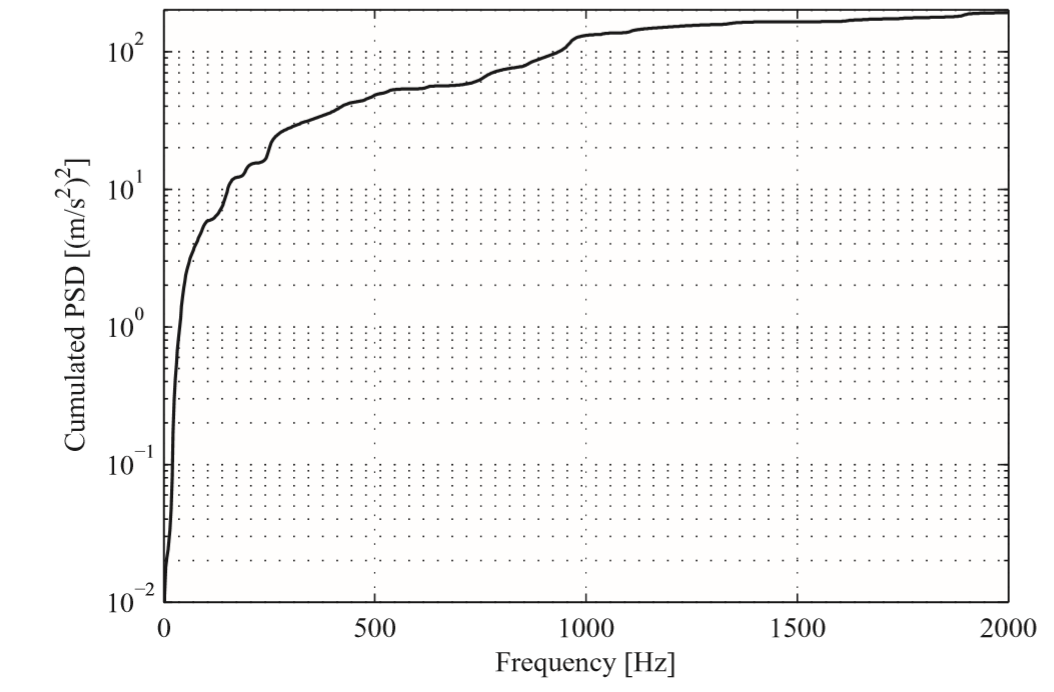
如上图左侧，可以得到任意频率之间的RMS值，也可以得到整个频段的RMS值；右侧是RMS cumulated。也就是RMS在各频率的逐步累加图的显式。最后一个频率下累加的RMS就是整个频段下RMS值。

RMS结果的解读

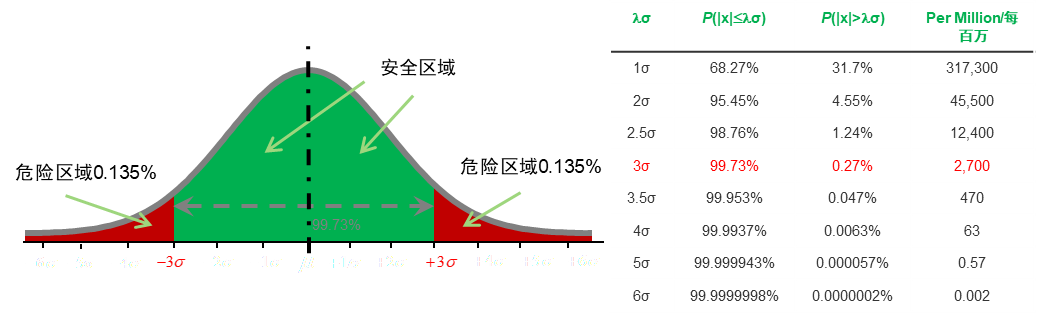
根据随机振动结果，知道了RMS值之后，可以基于高斯分布的基本特性知道如下信息：

也就是响应分布在1RMS范围内概率是68%；2RMS范围内的概率是95%；3Sigma范围内的概率是99%。

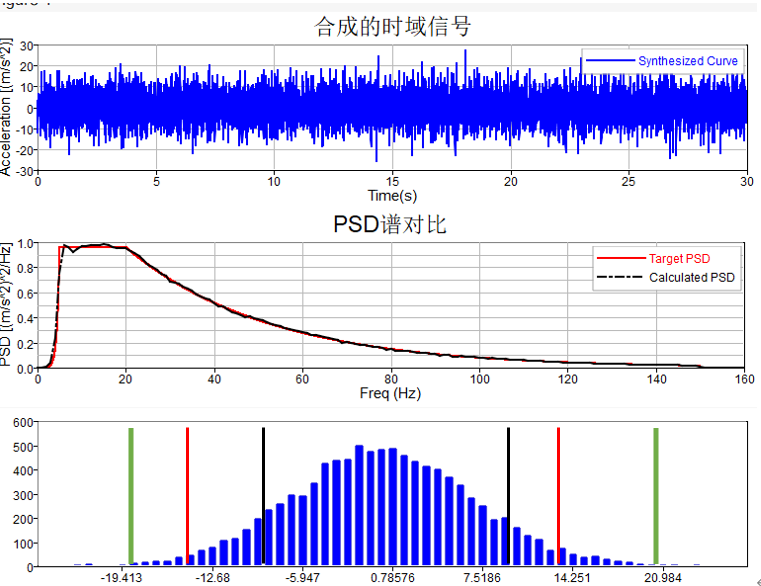
也许在时域里会更加有助于理解，下图是将我们的PSD响应给其一个随机的相位信息，通过傅里叶逆变换得到的一个时间历程曲线（可以认为是随机过程中的一个样本）。

中间是我们得到的PSD响应，该响应RMS为6.73；其逆变换得到的时间历程曲线见上，可见均值为0；最下图为该时域响应幅值在各个区间的直方图统计，可见基本呈正态分布。

响应分布在1σ（6.73）内的分布如黑色竖线以内，概率为68%；在2σ（13.4）内的分布如红色竖线以内，概率为95%；在3σ（21）以内的分布如绿色竖线，概率为99%。

也就是说，在某个随机激励工况下的响应有99%的概率在21以内。

当然我们可以根据其他概率目标确定应力的分布。

随机振动分析结果输出控制卡片示例如下，以应力说明：

Stress（PSDFC，H3d）= all

得到的结果会有以下几类：

1. PSD Stress

随机振动分析得到的应力功率谱密度曲线

PSD stress结果为曲线，即PSD Stress Vs.Freq 的曲线，PSD stress的单位为：Mpa^2/Hz。其结果可描述每一个频率下其应力的“功率或者能量”。所谓应力的能量可以理解为单纯的应力的平方。

因此如果想知道在激励频率下其应力曲线，即应力谱（stress spectrum），则可以将PSD Stress乘以频率间隔△f，然后开根号。即：

Stress spectrum = sqrt（PSD Stress * △f）

对于应力谱的理解是比较容易的，可以归类为传统的频响分析，即描述的就是在某个激励频率下，其应力的幅值。比如：某个频率f1下对应的幅值为A，则其表达的就是：

Stress = A*cos（2*π*f1）

即如果激励在f1频率下稳定激励时，结构的应力响应会是A。上式与传统的频响分析结果比较可见，缺少了相位。这是比较明显的差别，也可以理解为随机响应分析的“随机性”体现在相位上。

这里需要说明的一点就是，这里得到的应力谱其幅值为RMS格式，即A/sqrt（2）。

一般对于随机振动来讲，我们不是关心某一个频率下的应力，而是关心整体的应力标准差，或者说是应力分布区间，也就是RMS应力。而利用PSD stress可以提供给我们基本的优化思路，如果要减小rms应力，那么应该要重点降低那个频率下PSD应力，方便我们诊断问题。

RMS应力与PSD应力上文都有描述。

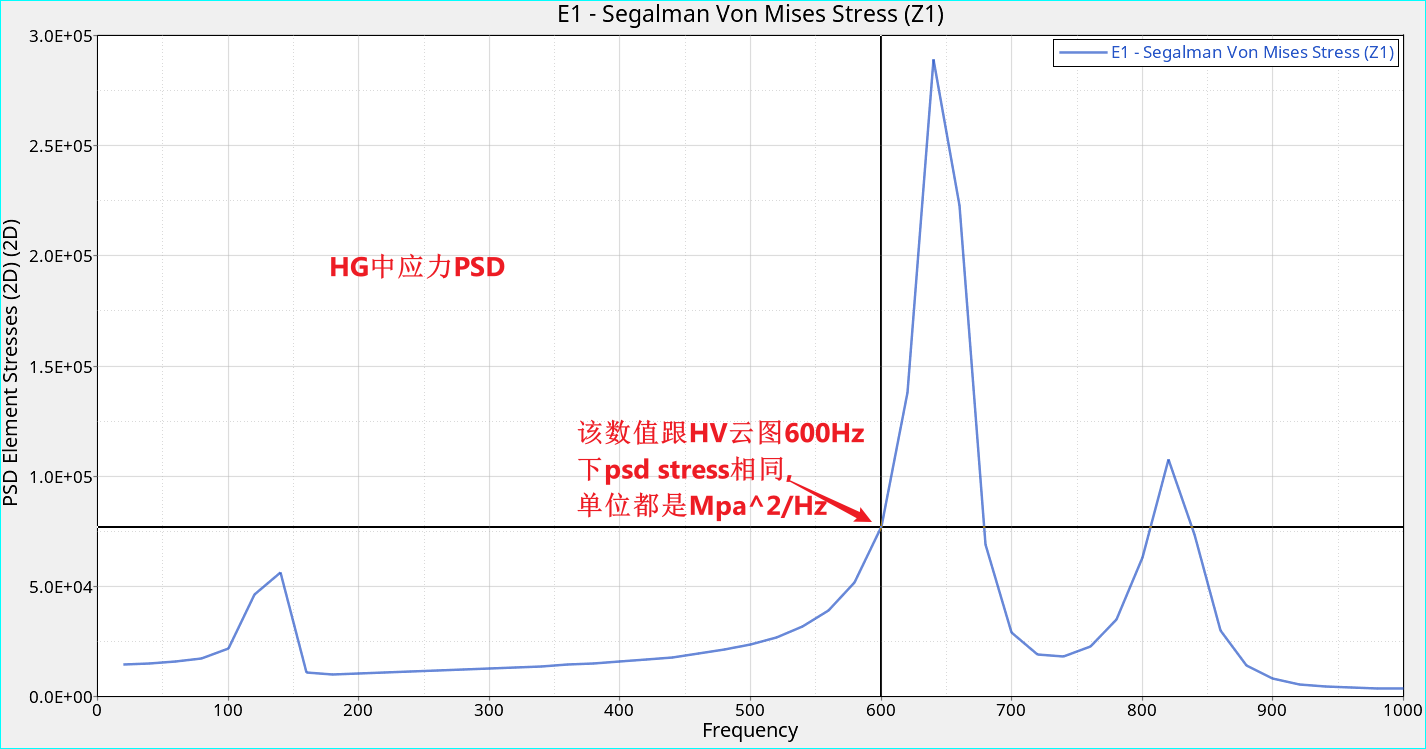
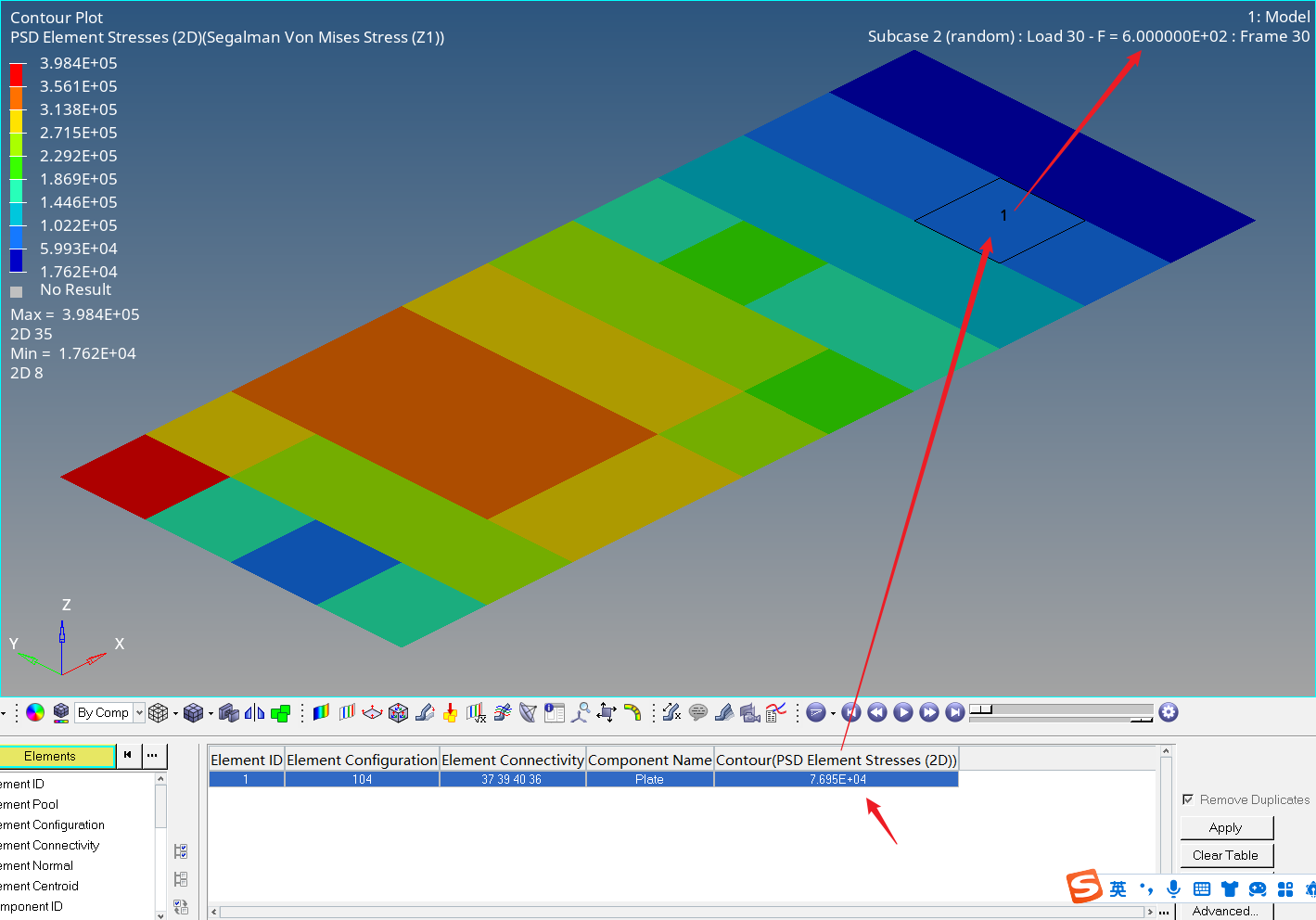
（胡建炜注）PSDF输出应力PSD谱，HV云图的结果单位也是MPa^2/Hz。

输出的psd应力谱通过HG打开，单位为MPa^2/Hz，该曲线积分后开方等于RMS值。当用HV打开h3d文件时，云图中各频率的应力数值跟psd应力谱一致，即HV中的云图PSD单位也是MPa^2/Hz。

1. RMS Stress

RMS（1σ）应力即PSD stress 下面积开根号，其结果归类为 “RMS over frequencies”结果 ；如果要想得到3RMS结果，则直接数值计算乘以3即可。

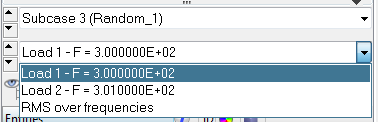
RMS Cumulated | RMS累加值

RMS累加结果,输出到该频率下的RMS累加结果 例如, “RMS displacement (cumulated)” for freq=100Hz ，输100Hz以前的位移RMS累加结果，单位为[mm]。

当RMS累加至最后一个频率时其值就等于RMS over Freq的值。