显式求解器和隐式求解器是啥意思?显式分析,隐式分析区别+弧长法
显式、隐式,看上去都是很高大上的词汇,行外人停了就懵逼了,行内人也乐得装逼。新手CAE小白也是一知半解。那他们到底是什么意思呢?
学理工科的,研究生时候会有一门课程,应该是叫做《数值分析》。数值分析分析的是啥呢,就是在教你解方程的方法。很多工程问题,通过理论可以列出一系列约束方程,怎么解这种方程呢?很多方程是无法像f(x)=2x=3能够直接反算出来x=1.5的,这就需要数值逼近方法来求解。
常见的案例,是下面这个图。这个图你可能看到很多遍了,但是很多老师其实都没解释清楚,你也就一知半懂的。
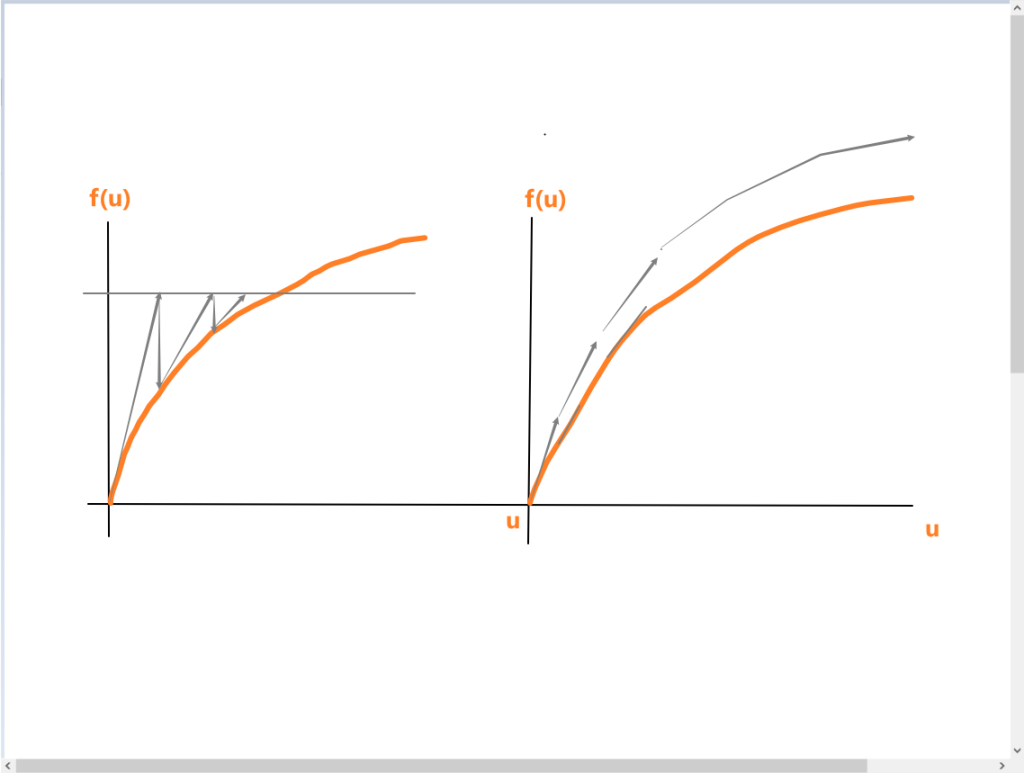
这个图是要干嘛呢?当我们有个工程问题他的简化方程是f(u)=F,其中F是外载荷,u是结构的变形。通过这个方程我们要干嘛呢,我们的目的,是求出加载F的情况下,结构的变形u。很多人光解释这个图,不去说最终的目的,听的人懵懵懂懂,这种老师也是在谋财害命。
我们的已知条件是什么呢?很多人看到这个图,以为橙色的线条是已知条件,那还数值计算个什么,线你都知道了,要求解某个F下的u,直接一读不就出来了吗。
真实的情况是,我们只能在每个猜测的u处,计算出其f(u),以及其梯度f'(u)。所以,就产生了显式和隐式这两种方法。
第一种隐式,先从起始点(0,0)开始,计算其梯度,确定切线和横线F的交点u1值,再计算f(u1),f'(u1),这样,从(u1,f(u1))点开始的切线,和横线F又有一个交点,其横轴坐标u2,继续这个路子迭代u1,u2,u3…,un,直到u值不再变化,即认为收敛,收敛后的un值,就是需要求解的真实变形u。这里面的F可以分成多段,比如想求解的F=100N下的位移,可以分10步来算,每步算10N。隐式分析的计算效率,主要是卡在了刚度矩阵求逆的过程,KU=F,K就是上面说的切线斜率,这时候要确定下一个U1点的δu,就需要K^-1求逆,对于几十几百万自由度的CAE模型来说,这是很费时间的。这种迭代求解的方法,就是常听到的牛顿-拉夫逊法(Newton-Laphson)迭代,也叫做牛顿法。
第二种,显式求解。同样从(0,0)开始,计算其梯度,做切线,但切线的横轴跨度,永远是很小的δu,这样到u1=δu时,重复这个操作,可以看到出来的曲线就是贴着真实的橙色线走的。可以发现,这种方法的出来的曲线永远和真实曲线是偏离的,所以需要保证δu足够小,以保证偏离地不会太远。通常来说,仿真碰撞这种工况,比如100ms,这时候的δu会设置成e-7这个级别。所以显式分析虽然简单粗暴,就是往前干,但是求解步非常多,导致求解速度很慢。需要注意的是,右边那条曲线没有表现时间的概念,因为显式求解问题通常伴随很大的加速度,所以时间的积分效应不可避免。每一步向前推进,加速度积分可以得到速度,也就是图中的斜线梯度,所以说本质就是切线步进,且每一步的物理量都是可以通过前一步物理量显性地直接计算得到,所以叫做显式算法。
显式求解、隐式求解分别适用哪些分析?
说了显式、隐式分析的方法本质差别,那这两种方法分别适用哪些场景呢?一般来说,隐式分析适用于静态或者准静态过程,即基本没有加速度的场景。如慢加载(抗凹分析,橡胶压缩回弹,螺栓预紧等),静态分析等。而显式分析适合加速度急速变化且接触状态高度非线性的场景,如爆炸、碰撞等。
常见的商业软件-显式求解器:Ls-Dyna,Radioss,Abaqus/Explicit
常见的商业软件-隐式求解器:Abaqus/Implicit,OptiStruct,Nastran,ANSYS
弧长法又是什么?
隐式分析中,有个选项叫做弧长法,在OptiStruct中的关键字是NLPCI(没记错的话)。他是用来干啥的呢,照例看下面的图。

上图是典型的后屈曲问题的载荷路径图。可以看到,用我们上面的牛顿法迭代,已经不能求出真正的图右侧的解了。困在B点的最终结果,就是落到B点,做切线就和F轴没有交点了,求解彻底发散。
运气好的话,可能可以找到右侧的点,如下图。可以找到正确的D点,但是要凑运气不够稳健。并且,对于B之后这一段(B和C纵坐标带宽覆盖这一段),牛顿法是无法计算整条路径(load-path)的,所以看结果的时候就会显得不连贯。
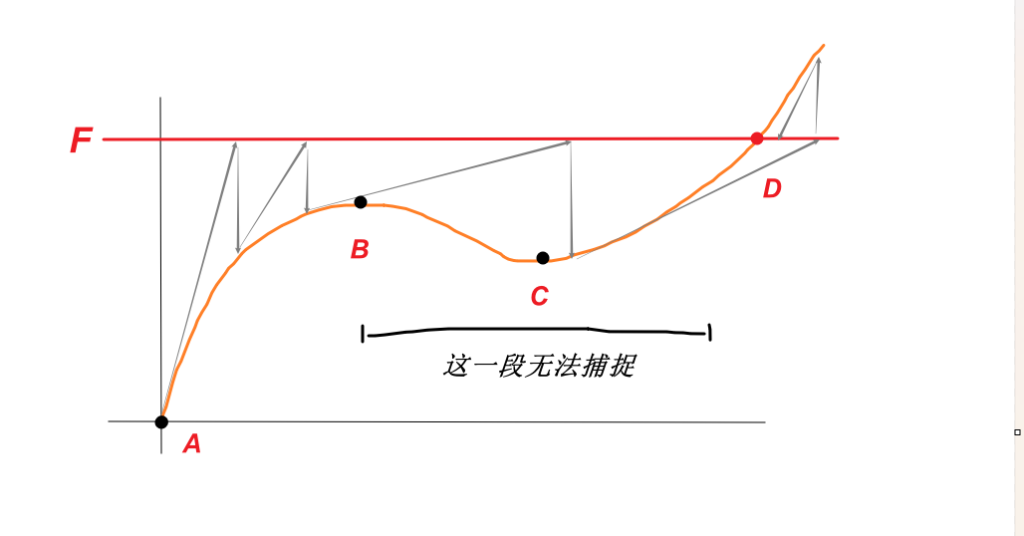
那针对这种问题,就开发了弧长法。它是怎么求解的呢?
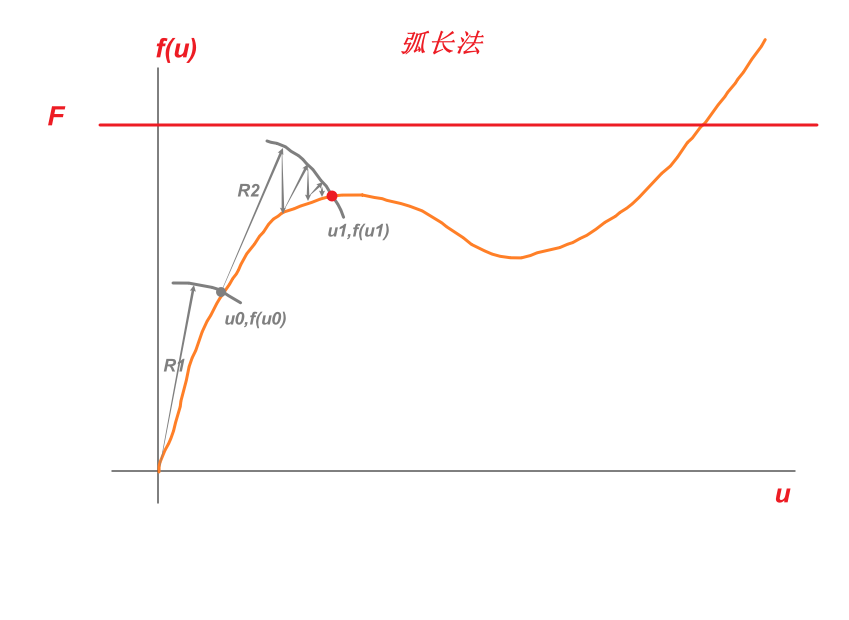
这个图中,每次切线就不去找和F横轴的交点了,直接假定一个半径范围Ri,这个Ri可以取F的系数,每次往前走Ri,找到下一个交点。这每一步的交点是怎么找的呢,其实用的还是牛顿迭代法。比如从(u0,f(u0))开始,半径为R2的圆,每次切线都去和这个圆相交,再不断跌倒,最后收敛到(u1,f(u1))点。画圆的好处是,就算碰到切线为水平的(即上上图中的B点处),这个水平切线也还是能够和圆有交点,从而继续迭代跨过屈服点,从而捕捉整条load path。